N-point DFT는 아래의 이전포스트에서 처럼, 다음과 같이 나타낼 수 있다.
DSP) Overlap-Add와 Overlap-Save 컨볼루션
디지털 신호 x[n]에 대한 주파수 성분을 나타내는 방식에는 두 가지 방법이 있다. DTFT 와 DFT. DTFT(Discrete Time Fourier Transform)은 주파수 축의 표기가 w(오메가)인 연속신호이고 DFT(Discrete Fourier Transform)
99kh.tistory.com
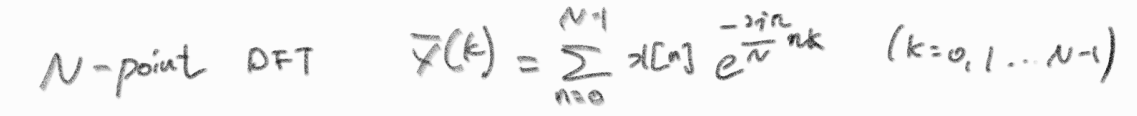
이때, 쓰기 복잡시러운 exp부분을 아래와 같이 줄여 쓰자.
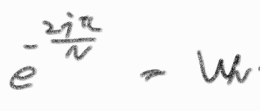
그럼, 예를 들어서 4-point DFT는 아래와 같이 나타낼 수 있다.
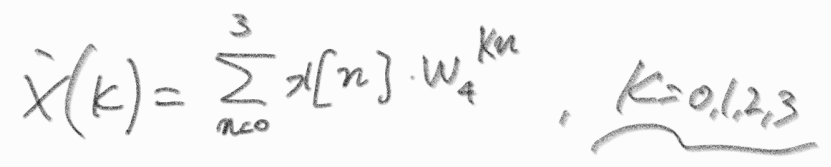
이 연산을 행렬로 표현하면 아래와 같다.
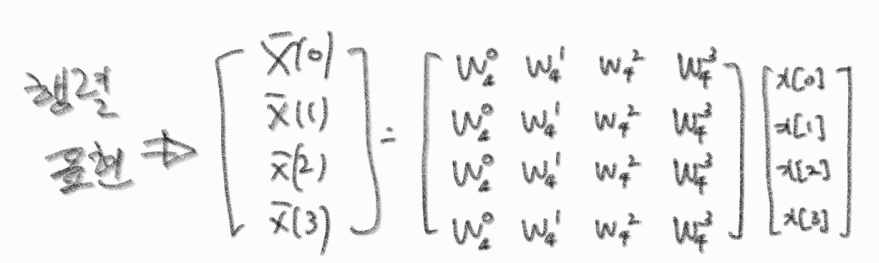
이는, 단순 행렬계산 시 4 x 4로 총 16번의 계산이 들어가야함을 알 수 있다.
그런데, 사실 W_4 이친구는 exp을 줄여 쓴 것이므로, a+jb꼴의 복소수다. 따라서 곱셈의 수는 16보다 훨씬 많아진다.
이러저러해서 N-point DFT의 연산 시에 고려해야 할 사항은 아래와 같다.

N-point DFT는 N^2번의 곱셈이 필요하다 ( 1의 곱도 곱셈으로 세었을 때) 이는 너무 많은 연산을 필요로 한다.
따라서, 곱셈 연산횟수를 감소시키기 위해고안한 알고리즘이
고속 푸리에 변환 (FFT : Fast Fourier Transform)
인데, 이는 크게 DIT(Decimation In Time) 와 DIF(Decimation In Frequency)로 나뉜다.
두 경우 모두 하나의 가정을 가지고 출발한다.
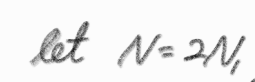
N = 2 x N_1 라고 하자.
1. At DIT,
이산신호를 짝수항과 홀수항으로 분해할 수 있다.

이때, 짝수항 x[2r]을 y[r]이라고 하고, 홀수항 x[2r+1]을 z[r]이라고 하자.
그럼, 총 길이는 N이지만, 짝수항 홀수항은 각각 N/2인 N_1이다.
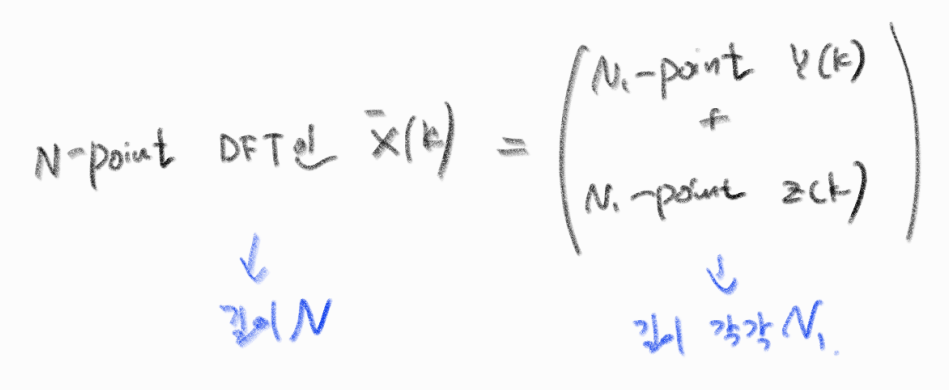
이때,
X(k)를 다시 쓰면,

와 같이 된다.
X(K)는 0부터 N/2 의 길이를 가지고, X(K+ N/2)sms N/2부터 N/2의 길이를 가져, 총 N의 길이를 가지는 X(k)가 구해진다.
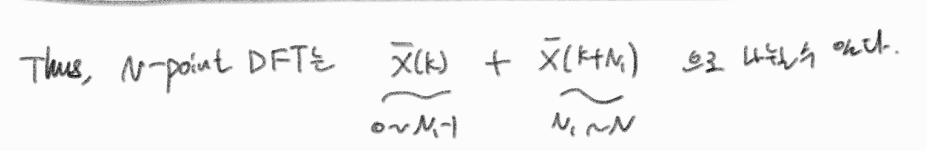
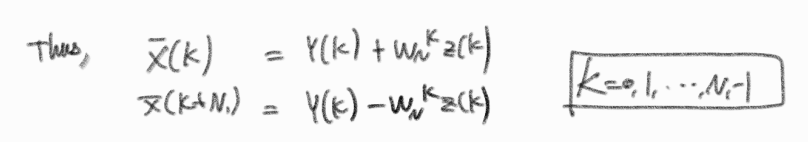
이다.
만약 8-point DFT를 하는 경우엔,
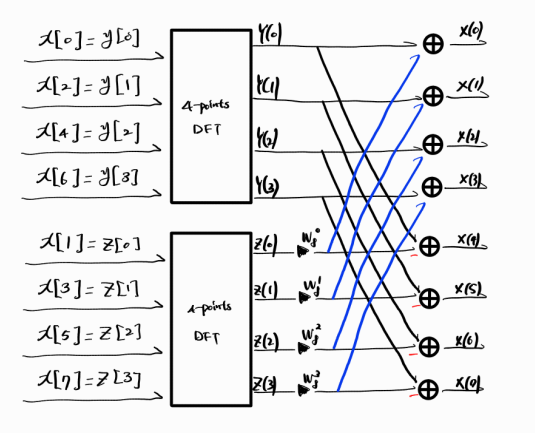
위 그림과 같이 두 개의 4-point DFT 합으로 나타낼 수 있고,
두 개의 4-point DTF는 각각 두 개의 2-point DTF로 나타낼 수 있어, 최종에는 아래와 같이 나타낼 수 있다.
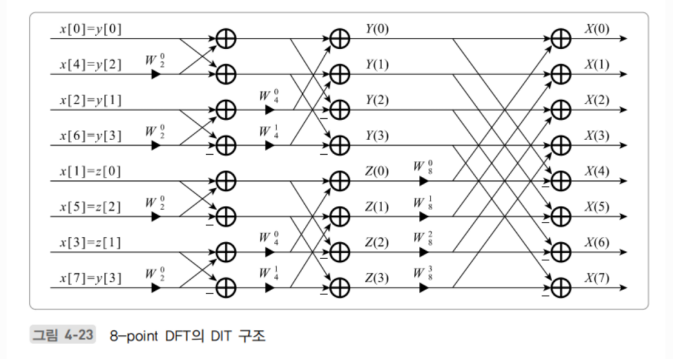
이러한 연산은 상술했듯이, 고속 푸리에 변환인데, 그렇다면 얼마나 연산이 줄어들까?
앞서 얘기했 듯, 그냥 DFT를 구하는 경우, 곱셈의 수는 N x N 즉, N의 제곱번 이다. ( 1을 곱하는 경우도 곱이라고 가정)
고속푸리에변환 DIT를 진행하는 경우, 각 계층(stage)마다 N/2의 곱셈이 존재하고, 계층(stage)는 log_2 (N)개 존재한다.
따라서 곱셈의 횟수는

이다.
글이 너무 길어져 다음 포스트에 글을 이어서 작성하겠다.
'전공공부 > 통신관련' 카테고리의 다른 글
| 디지털통신) PCM(Pulse Code Modulation) (1) | 2023.10.26 |
|---|---|
| DSP) 고속 푸리에변환 (FFT) (2/2) (0) | 2023.05.29 |
| 통신이론) AM변조기술 중 SSB (Single Side Band), USB, LSB (1) | 2023.05.14 |
| DSP) Overlap-Add와 Overlap-Save 컨볼루션 (1) | 2023.05.13 |



